
That's why it's fair to toss a coin to decide which football team gets to receive the ball and which has to kick off because both sides have an equal or 50% chance with a single coin toss. What is the chance of tossing a coin and having it land heads up (H)? Mathematically, the chance of H or probability of H on one toss of one fair coin (that has one head and one tail) is equal to the number of heads (H) divided by the total number of possible outcomes (heads plus tails, or H + T): Pr(H) = H/(H+T) or ½ or 0.50. It's also common to talk about the chance of occurrence, which is commonly described by percentage figures between 0.0% and 100.0%.Ĭoin toss examples. A probability of 0.00 means the event will never occur. A probability of 1.00 means the event will always occur. Probability is a number from 0.00 to 1.00 that represents the chance that an event will occur. You may have used probability theory in chemistry to predict the number of isomers for compounds containing asymmetric carbon groups. You may have used probability in your genetics class to construct a Punnet square. You most likely have already been exposed to the topic of probability in earlier courses.

In laboratory quality control, where it is common to make only two or three measurements, what is the probability of detecting medically important errors when using a Levey-Jennings control chart with control limits set as the mean plus and minus 2 SD? What is the chance of a false rejection, i.e., an out-of-control signal even though the method is working properly?
For example, in evaluating the performance of a new laboratory method by analyzing 40 specimens on a new method and a comparison method, what is the probability, or chance, that the difference observed between methods represents a real measurement error and not just a figment of the noise in the data (random error, imprecision, or scatter). Data is often limited because of cost considerations, therefore, it is very important to interpret that data properly. Probability is important because it helps us understand the chances of making a correct inference or decision on the basis of a limited amount of data. In fact, the road may be quite smooth once you understand probability and its usefulness for interpreting measurement data. Our objective in this lesson is to get by that roadblock and demonstrate that what lies beyond is not really so bad. Probability is one of those statistical terms that may cause a mental roadblock for students.
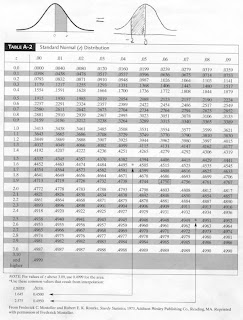
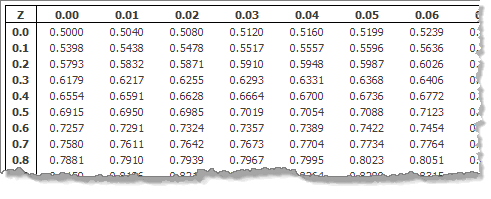
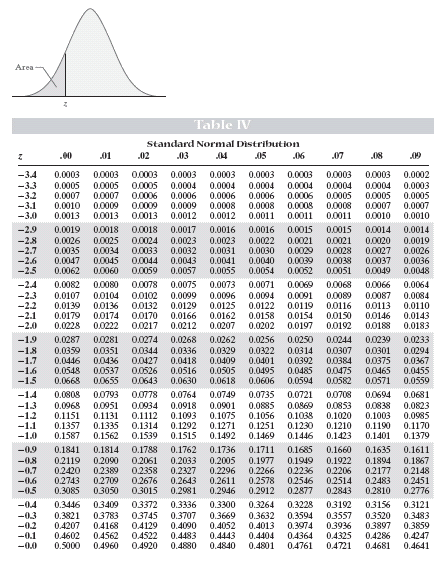
How z-scores can help us find probabilities. How a coin toss relates to laboratory testing.


 0 kommentar(er)
0 kommentar(er)
